Le blogue du jumeau numérique.
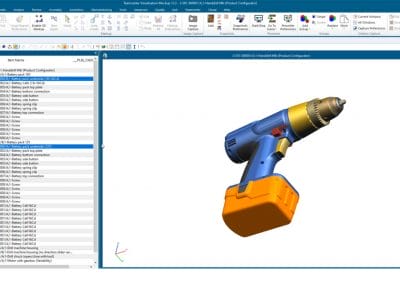
Quelle est la signification de PDM?
La Gestion de Données Produit (PDM), aussi appelé Product Data Management en anglais, est essentielle dans l'ère ...

Industrie 4.0 : Une Nouvelle Ère de Production
La révolution de l'industrie 4.0, marque un tournant décisif dans l'histoire industrielle. Depuis l'ère de la ...

M-Bot : votre propre agent conversationnel et votre bibliothécaire numérique personnel
Vous parcourez une myriade de documents techniques numériques afin de trouver une réponse à un problème?
Il est ...
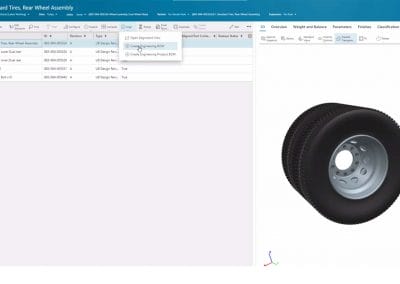
Quelles sont les nouveautés de Teamcenter 2312 ?
Teamcenter 2312 permet aux clients de gérer plus efficacement les conceptions et leurs processus ...

Quelles sont les nouveautés de Simcenter 3D 2312 ?
Simcenter 3D 2312 vous aide à rester intégré, à explorer les possibilités, à modéliser la complexité et à aller ...

Les tendances qui font parler d’elles : l’IA et l’AA au Realize LIVE
Le Realize LIVE, le tant attendu évènement annuel dédié aux utilisateurs qu’organise Siemens Digital Industries ...

Airborne Motorworks : Une technologie à propulsion électromagnétique permet la conception d’une turbine éolienne innovante
Le rêve de créer un véhicule volant a poussé Airborne Motorworks (AMW) à explorer le potentiel de ...
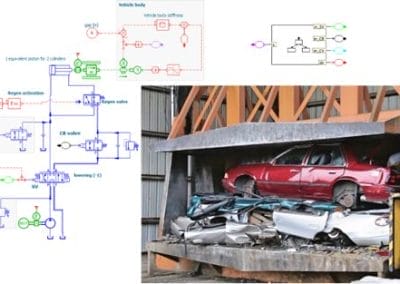
Conception d’un broyeur de voitures : des simulations système à la mise en service virtuelle
Parfois, un test d’acceptation usine révèle qu'une pièce d’un équipement ne fonctionne pas comme prévu. Cette ...
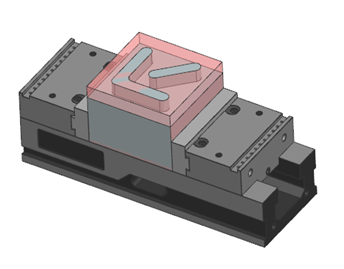
Usinage de cavité vs ébauche adaptative 3D et nouvelle méthode d’ébauche à grande vitesse
Comparaison des résultats de trois opérations 2,5 axes différentes
Les programmeurs CAM ont pour mission de ...
Les 10 principales choses que les fournisseurs de pièces doivent savoir pour passer de CATIA à NX Design
Lorsqu’un fabricant d’équipement d’origine décide d’adopter une nouvelle plateforme de CAO, cela se répercute sur ...
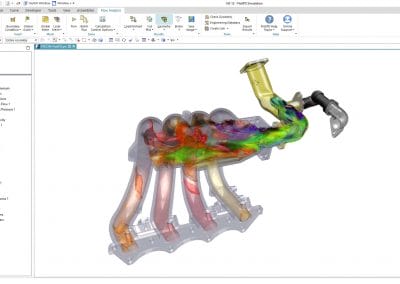
Les nouveautés de FLOEFD 2306?
Explorez les toutes dernières fonctionnalités de Simcenter FLOEFD, conçues pour permettre aux ingénieurs de ...

Nouveautés de Simcenter Amesim 2310 (simulation système)
Relevez facilement les défis quotidiens et gagnez du temps à chaque étape du processus d'ingénierie grâce à des ...